
「模型実験」って知ってますか?
”知っているか?”と突然問われると,ひっ掛け問題かと身構えてしまいますね.しかしながら,難しいことを尋ねているわけではなく,ここでは「模型実験」は,”実物による実験が難しい対象を評価するために模型を用いて実験する方法” と考えてもらって大丈夫です.
”実物で実験できない” 事情は様々ですが,最もわかりやすい理由は「サイズ」です.橋やダム,航空機や船舶など,実用上の失敗が決して許されない巨大な研究対象があります.一度つくったら何十億円以上も費用がかかり何十年も使い続ける上,一度事故が起これば何十何百の人命が奪われるので,これらの研究対象では「試し」も「失敗」もあり得ません.また,地震や津波などの大規模災害,公害や環境問題,プレートテクトニクス理論など,「広範囲の地形」といった実物を扱いようがない規模の研究対象もあります.したがって,こうした研究対象は,1/n倍の縮小模型を作成して,安全性や機能性を確かめる実験や理論検証を行うわけです.下図の瀬戸内海大型水理模型は,瀬戸内海周辺の地形が1/2000倍サイズで再現され,公害や環境問題の評価に利用され続けている模型実験の好例です.縮小されても地形模型は大規模になりますね.
大事故が起こると,1000年に1度の偶然だとか,数億分の1の確率だとか釈明を聞くことがありますが,こうした事故の原因は結局のところ「想定外の因子」です.コンピュータシミュレーションが発達した現在においても,”自分が想定できない因子” は計算式に組み込めないわけですから,「不測の事態」まで含めて安全性を評価できる「実験」はとても重要です.


なぜ,模型実験の話を?
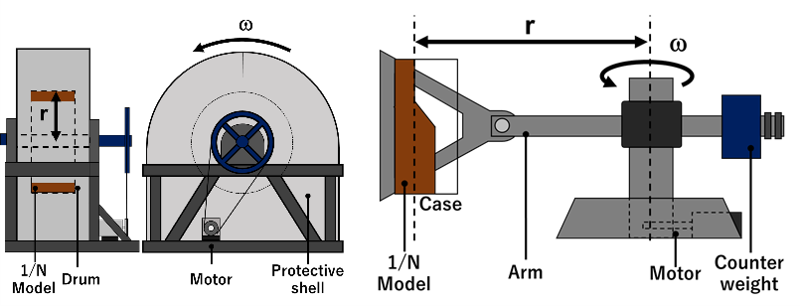
本題に戻りましょう.そもそも「重力」の話をしていたのに,なぜ「模型実験」を語っているのかといえば,高重力場を利用する模型実験法が存在し現役で利用され続けているからです.この知見をものづくりへ活用したい!ということです.この実験方法は,「遠心模型実験 (Centrifugal model test)」などと呼ばれ,フランス人技術者 Phillip が1869年に構想に着手したとされるほど長い歴史を持っています[1].1930年代には,米国,ソ連が世界恐慌を背景に公共事業を拡大するなかで,インフラ建設計画の需要に応えるように遠心模型実験に関する研究を盛んに行ってきました.第二次世界大戦の時期は論文発表などの情報が極端に少なくなりますが,1960年代から再び建築学や地質学の重要なテーマとして発展し,遠心模型実験は現在も様々な研究に利用されています.(「遠心模型実験」を検索ワードとして画像検索すると,建築会社,研究所,大学の各装置を確認できます! 興味深い巨大設備が並びますよ.)
実用例 (著作権の都合,リンクのみ張っておきます.)
〇 遠心模型実験装置の実例 (国立研究開発法人 海上・港湾・航空技術研究所 港湾空港技術研究所 リンク)
〇 スイス チューリッヒ工科大学にて建設中.2023年完成予定. (ETH Zurich リンク) →2023年オープンしました.リンク
中には10m近くの回転半径をもつものもある巨大実験装置です.これほどの巨大装置がなぜ必要なのかというと,”模型実験の重大な弱点”を補うためといえるでしょう.
遠心模型実験の相似則 (アナロジー)
”模型実験の重大な弱点” とは,「物理現象を単純に1/n倍に縮小できない」ことです.例として,建築物内の大きな梁を想定して,1/n倍模型で実験を行うとしましょう.実験目的は,「実際に梁がどれほど歪むかを確かめること」とします.
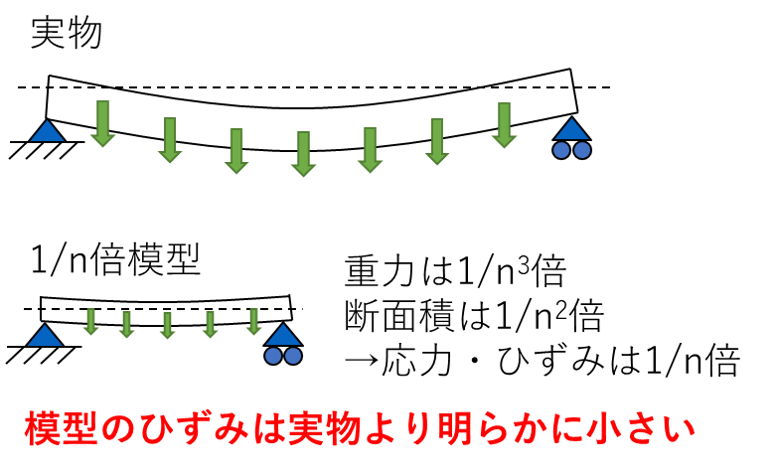
まず,梁を1/n倍サイズに縮小すると体積は1/n3倍になるので,(密度)×(体積)で求まる「質量」,そして(質量)×(重力加速度)で求まる「重力」も 1/n3倍になります.一方で,面積は 1/n2倍になるので,「梁の断面積」は 1/n2倍です.梁にかかる「応力」は,(応力) = (力)÷(面積)なので,1/n倍模型で自重によって梁に生じる内部応力は,( 1/n3倍の力)÷( 1/n2倍の面積) = (1/n倍の応力) となることがわかります.これでは歪みも1/n倍になってしまい,実物の歪みと対応が取れなくなってしまいます・・・.
そこで建築学で考案されたのが,1/n倍模型にn倍の重力加速度を加える実験方法でした.1/n倍模型にn倍の重力加速度を加えると, 1/n3倍となっていた重力の減少割合は, 1/n2倍となります.これにより,自重によって梁に生じる内部応力は,実物と比較して1倍(つまり,同一)になります! 歪みも1倍となり,1/n倍模型は実物と比べて,1/n倍に”相似的”に縮小された変形を見せるわけです.
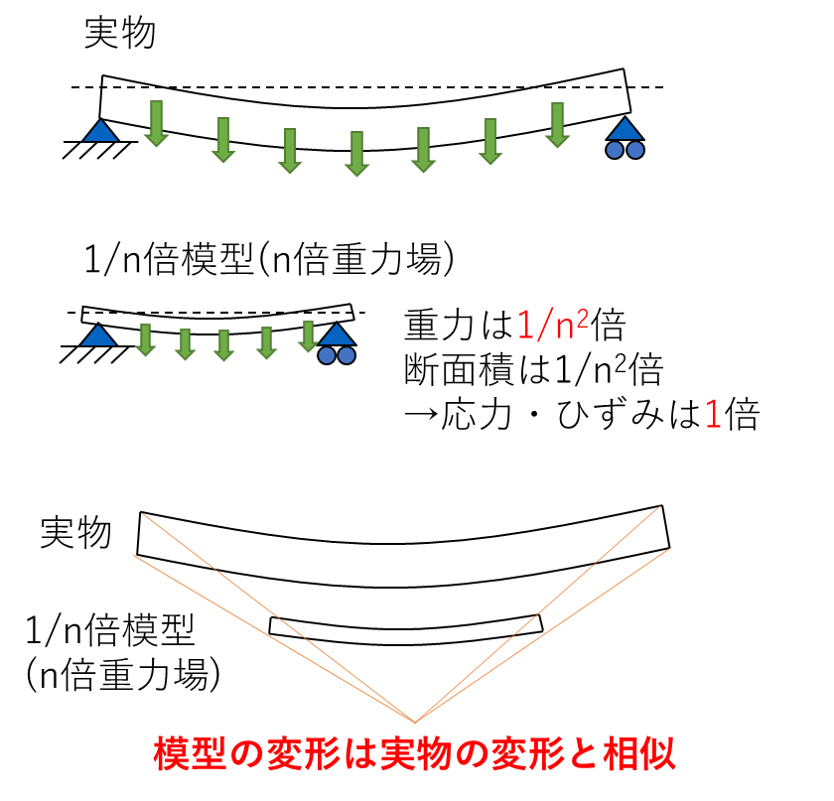
このようにして,1/n倍模型上で,1/n倍に縮小した物理現象(この例では構造物の弾性変形)を起こすわけです.n倍重力場における1/n倍模型に生じる物理現象を説明するために,各パラメータの変化量をまとめた表が以下のようになります.実際にはもう少し考慮すべき内容もありますが,それはこのページの下の方で補足説明をまとめます (現在編集中).こうして巨大構造物を実際につくることなく,安全性を評価することができます.とくに近年の世情から,地震や地盤沈下などの地質学的な問題の評価に活用できるために,遠心模型実験の注目度が少し高まっているようにも思えます.
| 遠心模型の相似則 | 実プロセス | 1/n倍模型 n倍重力場 | 各パラメータの倍率をまとめています. |
| 密度 | 1 | 1 | |
| 距離・変位 | 1 | 1/n | |
| 速度 | 1 | 1 | |
| 加速度 | 1 | n | 力と質量の関係から,加速度はn倍になります. |
| 質量 | 1 | 1/n3 | |
| 力 | 1 | 1/n2 | |
| 応力 | 1 | 1 | ここを1倍にしたかったわけです. |
| ひずみ | 1 | 1 | ここも1倍にしたかったわけです. |
| 時間(動的現象) | 1 | 1/n | 時間の進み方も変わります.詳細は次項目で. |
| 時間(浸透現象) | 1 | 1/n2 |
さて,結局この話がものづくりにとってなぜ魅力的なのかと言いますと,
「n倍重量場で物理現象を1/n倍にできるということは,加工精度も1/n倍にできる!」
・・・はずだと,小池は主張したいわけです.しかもこのnに入る数値は,洗濯機でもn > 50,超遠心機では n > 1,000,000という途方もない数値でしたね.第3次産業革命期でも加工分解能を1/1000倍にするのに20年以上の時間が必要だったことを考えると,高重量場が提供できる付加価値は,生産工学にとって極めて革新的です.
模型実験はあくまで,モデル化,解析次元の議論であり,最終的には実物の運用を成功させることではじめて意義を示せます.しかしながら,生産工学においては「物理現象を1/n倍に縮小する理論」そのものが,今の技術でつくれないものをつくる技術になる,といったものづくりにおける至高の価値に直結します.
次項目では,3Dプリンタに高重力場を付与するためのモデル化と,小池研が提案する新たなアナロジーについて語ります.
次項目:「相似則」とものづくり
出典
[1]五十嵐寛昌,遠心力を利用した模型実験,実験力学,Vol.2,No.4,pp.227-234, 2002.
(補足資料作成中.寸法効果,バッキンガムのπ定理)
