
ものづくりに「相似則」を当てはめてみよう.
遠心模型実験の理論は,梁や土嚢などの構造物をモデル化して,説明されることが多いです.液状化現象など流体が関わるモデルもありますが,ここでは割愛します.小池研究室にとって本題は,「n倍重力場で物理現象を1/n倍にする」理論が,ものづくり,とくに3Dプリンタでも当てはまるのか,という点です.
ここでは,粉末を利用する金属3Dプリンタの一方式,粉末床溶融結合 (PBF: Powder Bed Fusion) を対象に考えてみましょう.下図にあるとおり,薄い粉末層を敷いて,レーザ照射により選択的な溶融・凝固を生じさせ,1層ずつ積み重ねて所望の形状を造形します.つまり,造形物の加工精度を高めるためには,「いかに1層あたりの高さを低くできるか」が重要な課題となってきます.
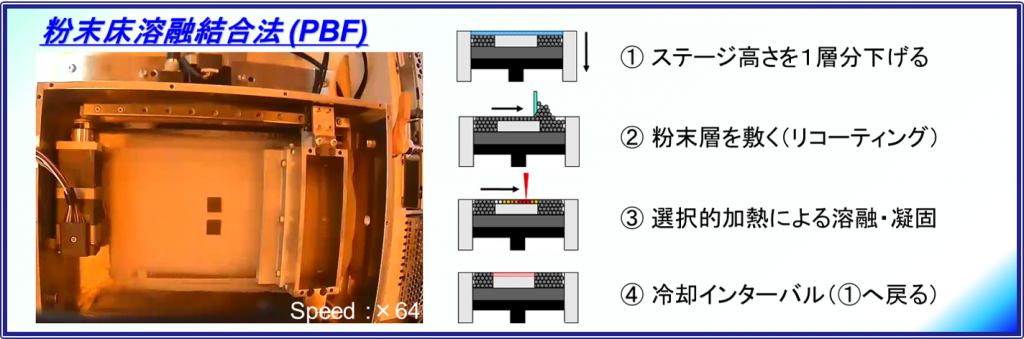

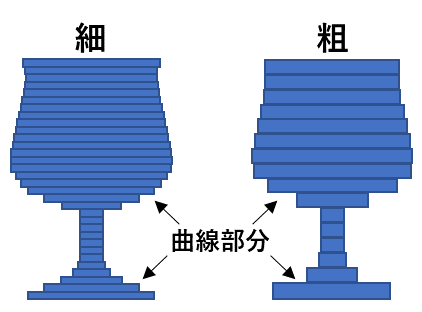
PBFにおける1層あたりの高さは一般的に,20 μm ~ 100 μm 程度です.この数値は,使用される粉末の粒径(直径) が 30 μm程度であるために必然的に決まってしまいます.「それなら,もっと細かい粉末を使えばいいでしょ」と皆さん考えると思いますが,そう簡単にはいきません.たとえば,実際に7.5 μm のステンレス粉末を造形台に敷いた様子を示すので見てください.

粉末が凝集し,ひび割れのようなものが発生して,まったく平坦に敷けないことがわかります.細かい粉末はわずかな風でも空気中に舞うなどの危険性もあります.身近な経験としては,料理中に小麦粉や片栗粉が空気中に舞ったりダマになったりするのと原理は同じです.また,PM2.5という大気汚染物質は有名だと思いますが,これは「particulate matter 2.5 (2.5 μm の粒子状物質) 」のことであり,粒子がここまで細かくなると国外から海を渡って飛散してくるほどの拡散性をもちます.こうした問題が起こりにくい最小粒径が 30 μm 程度だと経験的に知られているため,これより細かい粉末は使われないのです.
「プロセス寸法縮小効果」
しかし,経験則で満足しては学問になりません.PBFの力学的なモデルを考えるなら,プロセスが粉末粒子の運動の組み合わせで構成されていることから,粒子一つあたりにはたらく力を議論すべきです.このとき「はたらく力」は多様な候補が考えられますが,ここでは説明を簡潔にするために,静電気力,流体力,重力,浮力を議論しましょう.
相似則(アナロジー)を考えるために,粒子の直径が1/n倍になる状況を想定します.上述のとおり,PBFにおいて材料粉末の粒子は様々な力を受けるのですが,あるルールに従ってこれらの力を分類することができます.まず,電気的な力は粒子の表面積に比例することが多く,下図の2粒子間の引力としてはたらく静電気力は,粒径が1/n倍になると,1/n2倍になります.同じく,流体から受ける力には,揚力や抗力があり,代表面積や表面積と比例関係にあります.このように力の大きさが面積に比例する力を総じて,流体力学などでは「面積力」と呼びます.一方で,重力や浮力のように体積に比例する力は「体積力」と呼ばれます.これらの大きな違いとして,粒径が1/n倍となったときの減少割合が,体積力は1/n3倍,面積力は1/n2倍となるように,体積力は1/n倍余計に減少することがわかります.つまり,”ある粒径” よりも小さくなると,粒子を地面に押さえつける重力よりも,凝集を起こす静電気力や空間へ飛散させる流体力の方が大きくなり,PBFで粉末材料を扱えなくなります.そして,その “ある粒径” が30 μm 程度というわけです.
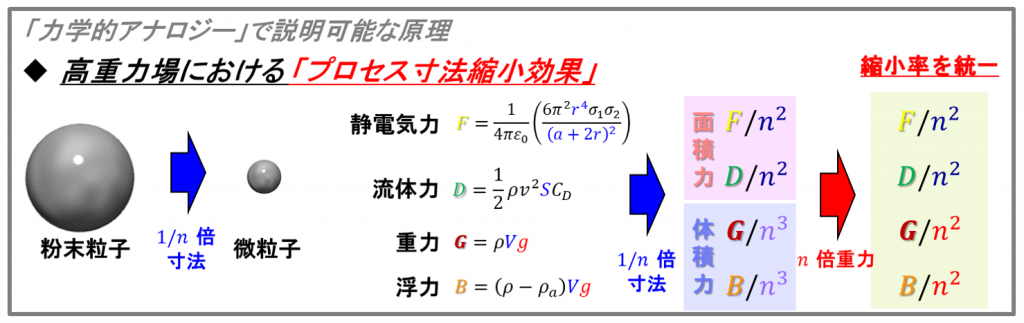
面倒でもこの過程を経ることで,重要な気づきを得られます.それは,「体積力の多くに含まれる”重力加速度係数g” が,面積力のほとんどに含まれない」ことです.このことから,重力加速度係数がn倍となる重力場において,それぞれの力の減少割合を1/n2倍に統一できます! 拡大・縮小の割合が統一されるときに思い出すのが,数学で習った「相似」です.力の方向が幾何学的に変わらず,力の減少割合が同じならば,1/n倍サイズの粒子の加速度ベクトルは元の粒子と同じ方向に向きます.これにより,1/n倍サイズの粒子で元の粒子運動を再現できます.
PBFプロセスがこれら粒子運動の組み合わせで構成されていることを考えると,プロセスサイズは確かに1/n倍にできますね.PBFで1/n倍サイズの粒子を使えるということは,1層あたりの高さも1/n倍にできます.レーザスポットの絞り込みは別技術ですが,高分解能化にあたって最も大きな障害となっていた「微細粉末の安定利用」の問題をみごとに解決できます!n倍重力場で得られるこの効果を「プロセス寸法縮小効果」と名付けました.
しかし,気づいた人もいるかもしれませんが,この説明では不都合な点に触れていませんね.粒子の加速度が大きくなりすぎることです.この問題の詳細と解決策を下にまとめます.
「プロセス時間短縮効果」
ニュートンの運動方程式は知っていると思います.いわゆる, ニュートンの第2法則とも呼ばれる,(力) = (質量) × (加速度) の式です.上記の1/n倍サイズの粒子における縮小倍率の議論では,力が1/n2倍となるように調整し,質量が1/n3倍になっていました.これをニュートンの運動方程式に当てはめると,加速度はn倍になってしまいます.つまり,元の粒子と比べると,同じ時間内でn倍の距離を移動してしまうのです.「この世界の物理現象を1/n倍にする」というコンセプトならば,移動距離も1/n倍になってもらわないと困りますよね.
この不都合の解決策は,じつは前項目で示した「遠心模型の相似則表」に書かれていました.ここにもう一度その表を示すので,確認してください.
| 遠心模型の相似則 | 実プロセス | 1/n倍模型 n倍重力場 | 各パラメータの倍率をまとめています. |
| 密度 | 1 | 1 | |
| 距離・変位 | 1 | 1/n | 変位は1/n倍になっています! |
| 速度 | 1 | 1 | |
| 加速度 | 1 | n | 加速度はn倍になります. |
| 質量 | 1 | 1/n3 | |
| 力 | 1 | 1/n2 | |
| 応力 | 1 | 1 | |
| ひずみ | 1 | 1 | |
| 時間(動的現象) | 1 | 1/n | 時間が1/n倍とは・・・? |
| 時間(浸透現象) | 1 | 1/n2 |
この相似則表,n倍重力場における1/n倍模型では,加速度がn倍となっていることを示しています.先の例では構造物の静的な弾性変形を挙げていたので,時間変化に関わる加速度と無関係な話でした.しかし,遠心模型実験には模型に地震動を与えるなど,動的変化を評価するものもあります.こうしたときにn倍の加速度が生じるのですが,相似則表では速度が1倍,変位が1/n倍となっています! 明らかに整合性がないように見えますが,これを矛盾なく解釈する方法が,「時間の進みをn倍に早める」です.
粉末粒子を例にすると,下図のようになります.1/n倍粒子の運動は,元の粒子のn倍の加速度を持つため,時間当たりの移動距離はn倍です.しかし,移動距離を1/n倍にしなければならないので,1/n倍プロセスでは時間がn倍で進むと仮定します.より具体的に何が起こるのかを説明すると,1/n倍プロセスをn倍に拡大して撮影し,撮れた動画を1/n倍スロー再生をすると,元プロセスを撮影したかのような同じ動きが見れるということです.(光量や被写界深度が違うとか,上げ足は取らないでください.) 時間がn倍で進むことを物理的に解釈するには,時間パラメータ t を t/n に置き換えます.実世界で時間 t で終了するプロセスが, 模型の中では t/nの時間で終了するという意味合いになります.このとき,時間微分 dt も dt/n となることから, 加速度がn倍なら,速度は1倍,変位は1/n倍となることを矛盾なく定められます.この時間短縮について,ものづくりでは,プロセス時間を1/n倍にする可能性を秘めた効果であると考え,「プロセス時間短縮効果」と名付けました.1/n倍模型以外にも適用可能な効果にもなるので,その実例はこれからの小池研の研究で示していきます.
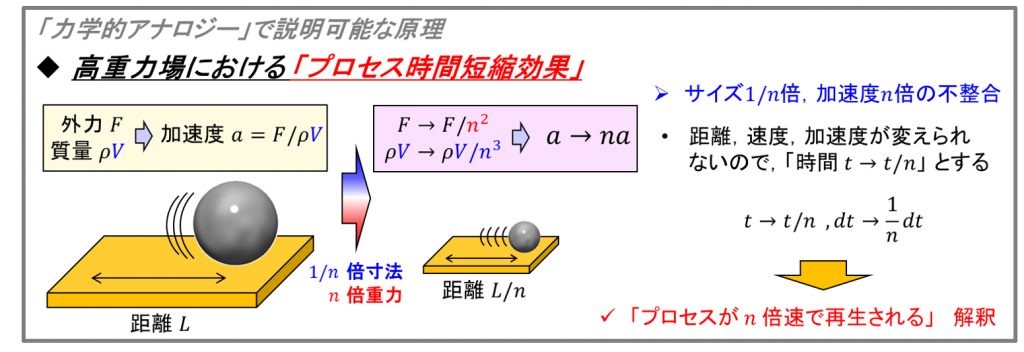
時間の進め方を変えるアイディアとして有名な理論には,アインシュタイン博士が発表した相対性理論がありますね.「光速を一定」に保つために,空間と時間を歪めてよいとする理論は,時空を絶対の尺度としてきた古典物理学から見たら驚くべき解釈でした.遠心模型実験も,「変位 (空間) を1/n倍」にするために時間を歪める理論といえますね.特殊相対性理論は1905年に発表されたようですが,遠心模型実験は1869年の基礎概念が構想されて以降,時間短縮の概念がどういったタイミングで着想されたかはわかりませんでした.しかし,まったくの異分野から工夫を取り入れた,もしくはまったくの異分野にアイディアを提供した,というようなおもしろい意外な関係があるかもしれません・・・.
説明が長くなってきたので,ここまでをまとめます.3Dプリンタに対してn倍重力場を付与すると,
- プロセス寸法縮小効果・・・加工分解能を1/n倍!
- プロセス時間短縮効果・・・造形時間を1/n倍!
といった効果が得られるということです.一般的に,「加工精度」と「加工効率」には,あちらを立てればこちらが立たず,いわゆる trade-off と呼ばれる関係があります.製品を丁寧につくれば時間がかかり,短時間でつくれば質が落ちるのは当然ですね.しかし,高重力場はこの常識に従わず,「加工精度」と「加工効率」を同時に高める効果があります.この trade-off を打破できる提案は学術的にも極めて珍しいので,画期的といえます.
少し長くなったので,現在の相似則の問題点は次項目で説明します.いよいよこのページで語らなかった,小池研の独自理論を展開していきます.
前項目:高重力場と模型実験
