
独自提案「異重力場の相似則」
いよいよ,小池研の独自提案についてです.研究背景としては,宇宙工学の発展,流体力学のπナンバーなどを絡めた話もあるのですが,今回の説明では独自提案に最もつなげやすい「模型実験」から話を展開しました.あとは,「模型実験」の歴史の中で扱われたことがない問題を説明するだけです.
遠心模型実験の相似則を示す際,力の大きさが体積に比例する「体積力」,面積に比例する「面積力」について説明しました.しかし,体積力でも面積力でもない,不都合な内容はあえて説明から外していました.具体的には,”ファンデルワールス力” と “表面張力” です.
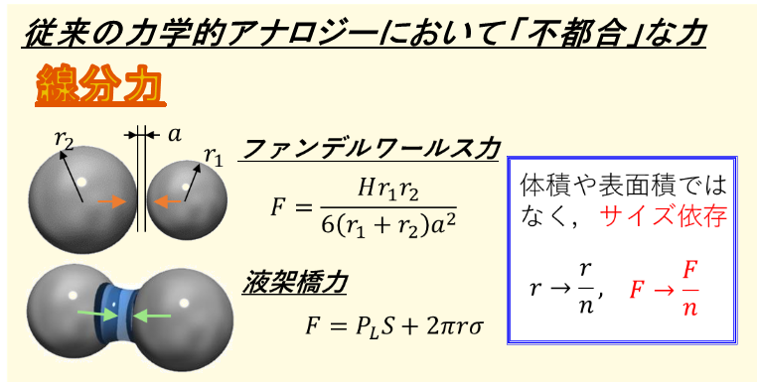
分子間にはたらく力として有名なファンデルワールス力は,上図のとおり粒子半径が1/n倍となると,その減少割合は1/n倍になります.また,液架橋力は,湿度が高い状況で右辺第1項が負圧項という面積力,右辺第2項が表面張力項という「サイズ」に比例した力であることがわかります.これらのサイズに比例する力を総じて「線分力」と呼びます.(流体力学の論文調査をした限り,「線力」といった言葉も使われるようです.このホームページでは「線分力」で統一します.)
ここで問題になるのは,粒径が1/n倍となるとき,線分力は1/n倍になるとおり,面積力や体積力よりもさらに減少割合が小さいことです.物理学のとくに力学を習ったとき,ファンデルワールス力は,「無視できるほど小さい」といってまともに扱ってもらえないことが多かったと思いますが,下図のとおり,1 μmのオーダー以下になると,もはや体積力こそ無視すべき力となり,面積力・線分力が支配的となってきます.
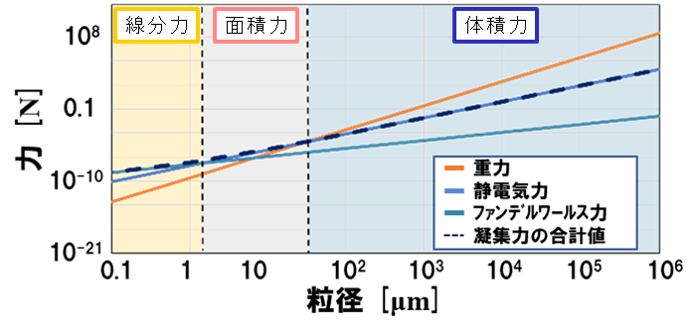
かつて多分野を横断して利用され続けた模型実験は,線分力が支配的となるマイクロの領域を扱わなかったといえます.構造の内部応力やひずみを調べる遠心模型実験ならば,n倍重力場を付与すればよく,ファンデルワールス力は無視すればよかったのです.しかし,面積力と体積力をもとに構築した相似則は,線分力が支配的な領域を議論できません.ここが模型実験の相似則の限界といえます.(・・・というよりも,模型は体感的に扱いやすいサイズに拡大・縮小してつくるものですから,マイクロサイズの模型をつくる需要はなさそうです.わざわざマイクロ領域を議論する必要性がなかったともいえますね.)
しかしながら,ここまでの話を読んでくださった皆さんなら,「線分力の支配領域では,n倍重力場の相似則が適用できない」という結論にはならないと思います.粒径1/n倍で線分力は1/n倍,体積力は1/n3倍となることから,体積力は1/n2倍余計に減少しています.それならば,ここで得るべき結論は「線分力の支配領域では,n2倍重力場の相似則を適用すべき!」・・・で良いですよね?
このように,線分力の支配域でn2倍重力場の相似則へ切り替えるハイブリッド相似則こそ,小池研独自の提案となります.この相似則を「異重力場の相似則」と名付け,以下の表のようにまとめました.
| 異重力場の相似則 | 実プロセス | 1/n 倍模型 n 倍重力場 | 1/n 倍模型 n2 倍重力場 |
| 密度 | $$1$$ | $$1$$ | $$1$$ |
| 距離・変位 | $$1$$ | $$1/n$$ | $$1/n$$ |
| 速度 | $$1$$ | $$1$$ | $$\sqrt{ n }$$ |
| 加速度 | $$1$$ | $$n$$ | $$n^2$$ |
| 質量 | $$1$$ | $$1/n^3$$ | $$1/n^3$$ |
| 体積力 | $$1$$ | $$1/n^2$$ | $$1/n$$ |
| 面積力 | $$1$$ | $$1/n^2$$ | $$※1/n^2$$ |
| 線分力 | $$1$$ | $$※1/n$$ | $$1/n$$ |
| 応力 | $$1$$ | $$1$$ | $$n$$ |
| ひずみ | $$1$$ | $$1$$ | $$n$$ |
| 時間(動的現象) | $$1$$ | $$1/n$$ | $$1/n\sqrt{n}$$ |
| 時間(浸透現象) | $$1$$ | $$1/n^2$$ | ー |
まず,遠心模型の相似則と大きく異なる点として,「n2倍重力場」の列が追加されています.先の図で,粒子サイズと支配力の遷移を示しました.ここまでの説明から,「体積力」か「面積力」が支配力の場合はn倍重力場の相似則を当てはめ,「線分力」が支配力の場合はn2倍重力場の相似則を当てはめることがわかると思います.
また「力」の行が,「体積力」「面積力」「線分力」の3つに分裂しています.n倍重力場の相似則を適用する際は,「体積力」か「面積力」が支配的なので,「線分力」は減少割合が小さくても無視します.(これまでの遠心模型の相似則でも,ファンデルワールス力は議論していないですよね.)そして,n2倍重力場の相似則を適用する際は,「線分力」を抑え込めるように「体積力」を高めることから,運動への影響が小さい「面積力」は無視します.(影響が小さい力としてn倍重力場の相似則が「線分力」を無視したように,「面積力」を無視する対応は問題ないと考えます.)このように「異重力場の相似則」は支配力によって法則を切り替えるハイブリッド理論であり,この切り替えによって1 μmオーダー以下の世界にも相似則を適用可能とします.
サブマイクロ,ナノオーダーの領域までアナロジーの開拓を行えるようにした新理論「異重力場の相似則」が小池研の提案であり,この理論の正しさと実用性を,3Dプリンタという研究対象を持って世界に発信する取り組みが小池研究室のミッションとなります.
ちなみに,慶應義塾大学理工学部システムデザイン工学科で最も重要視する概念に,「アナロジー」があります.システムデザイン工学教育の理念として,「調和性などの評価」「解析」「設計・合成」の3次元の広がりから,「解析」「モデル化」「新しい価値の創出」を実現できるシステムをデザインする人材の育成を目指しています.高重力場を利用する模型実験は,あくまで「評価したいシステム」の「解析」「モデル化」までで議論が止まったしまうのですが,異重力場の相似則は,加工分解能・加工効率を飛躍的に高めるという「新しい価値」に直結する学問です.模型というバーチャル(仮想空間)ではなく,リアル(実空間)で生きる技術としても,3次元的な広がりを見せますね.このように,異重力場の相似則はSD科から発信する新しいアナロジーとして,小池研究室が世界を牽引するかたちで開発したい学術領域です.
参考:慶應義塾大学理工部システムデザイン工学科HP リンク
次項目で最後になります.あとは,高重力場が3Dプリンタに与える有益な効果について,小池研究室から発表された実験結果を簡単に解説していきます.
次項目: 高重力場と3Dプリンタ
前項目: 「相似則」とものづくり
